Transitive Graphs

a brief introduction

Automorphism

An automorphism of a graph $G=(V,E)$ is a bijective map $\pi:V \to V$ that preserves adjacency, i.e. if $(v_1,v_2)\in E$ then $(\pi(v_1),\pi(v_2))\in E$.

Example 1. An automorphism of the square graph defined by the permutation $\sigma=(1,2,3,4)$.

An automorphism of a graph $G=(V,E)$ can be seen as a permutation over its set of vertices $V$. The Example 1 shows an automorphism of the square graph, which is denoted by the permuation $\sigma=(1,2,3,4)$ (in cycle notation). Notice that $\sigma^2=(1,3)(2,4)$, $\sigma^3=(1,4,3,2)$ and $\sigma^4=(1)(2)(3)(4)$ are also automorphisms of the square graph.

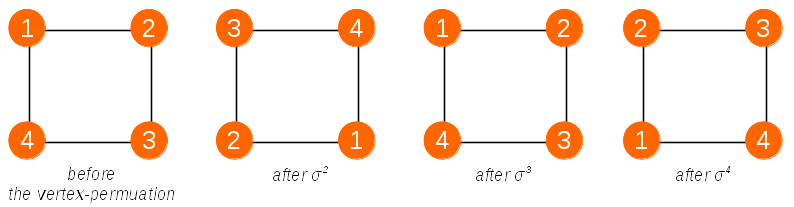
Example 2. The automorphisms of the square graph defined by the permutations $\sigma^2$, $\sigma^3$ and $\sigma^4$.

Here, we have two interesting questions:

1. Do all graphs have any automorphism?
2. What is the maximum number of automorphisms that a graph can have?

The answer of the first question is yes, all graphs have at least the trivial automorphism, denoted by $\varepsilon$, that maps each vertex to itself. As we can see in the Example 2, $\varepsilon=\sigma^4$. Turning now to the second question, since an automorphism is defined by a permutation over $|V|$, then a graph has at most $|V|!$ automorphisms, it is the number of permutations over $V$. For instance, the set of automorphisms of the square graph is $Aut(G)=\{\varepsilon, \sigma, \sigma^2, \sigma^3, \rho, \tau\}$, where $\rho=(2,4)$ and $\tau=(1,3)$. In particular, for the complete graph of $n$ vertices, i.e. $K_n$, any permutation over $V$ define an automorphism, for instance $|Aut(K_3)|!=3!=6$.

Example 3. The complete graph $K_3$ and $Aut(K_3)=\{\sigma,\sigma^2,\sigma^3,\rho,\tau,\phi\}$ where $\sigma=(1,2,3)$, $\rho=(1,3)$, $\tau=(2,1)$, $\phi=(3,2)$.

Lectors familiarized with algebraic groups can see that $Aut(G)$ has a group structure with respect to the composition of functions, where $\varepsilon$ is the identity element. In fact, $Aut(G)$ is a subgroup of the symmetric group which consists of the set of all permutations of a set.

Vertex-transitive Graphs

A graph $G=(V,E)$ is vertex-transitive if there is an automorphims between any two of its vertices, i.e. for all $u,v \in V$, there exists $\pi \in Aut(G)$ such that $\pi(u)=v$. Notice that the graph of Example 1 is vertex-transitive. Now, look at the graph of Example 4, is it vertex-transitive?.

Example 4. The 3-path graph with the automorphism $\sigma = (1,3)$ and $Aut(G)=\{\varepsilon, \sigma\}$

Roughly speaking, all vertices in a vertex-transive graph have the same “graph perpective”. In Example 4, vertices $1$ and $3$ are the end points of the 3-path, then they have the same “graph perpective”. In fact, $\sigma$ defines an automorphism between these vertices. By the other hand, the vertex $2$ is an internal vertex of the 3-path, then it has a different “graph perpective” and it is not possible define automorphism over the 3-path that maps the vertex $2$ to the vertex $1$ or $3$. Therefore, the 3-path is not vertex-transitive.

In general, all vertex-transitive graph are regular but not all regular graphs are vertex-transitive.

Edge-transitive Graphs

A graph $G=(V,E)$ is edge-transitive if there is an automorphism between any two edges, i.e. for all $(u,v), (w,x) \in E$, there exists $\pi \in Aut(G)$ such that $(\pi(u),\pi(v)) = (w,x)$ or $(\pi(u),\pi(v)) = (x,w)$.

From Example 4, $E=\{(1,2),(2,3)\}$ and $(\sigma(1),\sigma(2))=(3,2), (\sigma(3),\sigma(2))=(1,2)\in E$, therefore the 3-path graph is edge-transitive. Following a similiar approach it can be showed that the square graph (see Example 1) is also edge-transitive.

Example 5. A graph with the automorphisms $\sigma = (1,2,3,4,5)(6,7,8,9,10)$, $\rho=(1,6)(2,7)(3,8)(4,9)(5,10)$, $\tau=(2,5)(3,4)(7,10)(8,9)$ and $Aut(G)=\{\varepsilon, \sigma^i, \sigma^i\rho, \rho, \tau\}$ for $1\leq i \leq 5$.

Let see if the graph $G=(V,E)$ of Example 5 is edge-transitive. Let $E_1$, $E_2$ and $E_3$ be subsets of $E$, such that $E=E_1\cup E_2 \cup E_3$ where $E_1=\{(1,2),(2,3),(3,4),(4,5),(5,1)\}$, $E_2=\{(6,7),(7,8),(8,9),(9,10)\}$ and $E_3=\{(1,6),(2,7),(3,8),(4,9),(5,10)\}$. We have that:

• $\sigma^i\rho$ defines an automorphism from edges in $E_1$ to edges in $E_2$, e.g. $(1,2)\in E_1$ and $(\sigma(\rho(1)),\sigma( \rho (2)))=(\sigma(6),\sigma(7))=(7,8)\in E_2$.
• $\sigma^i$ defines an automorphism between edges in $E_1$ and $E_2$, e.g. $(3,4)\in E_1$ and $(\sigma(3),\sigma(4))=(4,5)\in E_1$. Similarly, $(7,8)\in E_2$ and $(\sigma^2(7),\sigma^2(8))=(9,10)\in E_2$.
• $\tau$ defines an automorphism between edges in $E_3$. e.g. $(2,7)\in E_3$, $(\tau(2),\tau(7))=(5,10)\in E_3$.

Since edges in $E_3$ are part of two cycles of length 4 and edges in $E_1 \cup E_2$ are part of two cycles of length 4 and 5, then it is not possible define an automorphism between them. Therefore, the graph of Example 5 is not edge-transitive. Intuitively, it means that edges in sets $E_1 \cup E_2$ and $E_3$ have a different “graph perpectives”. In contrast, this graph is vertex-transitive, note that all nodes are part of two cycles of length 4 and 5, then all nodes have the same “graph perpective”.

In contrast with vertex-transitive graphs, edge-transitive graphs are not necessarilly regular. However, if a graph is regular and edge-transitive, then it is also vertex-transitive.

Arc-transtive graphs

A graph $G=(V,E)$ is arc-transitive (also called symmetric or flag-transitive) if there is an automorphism between any two edges, i.e. for all $(u,v), (w,x) \in E$, there exists $\pi \in Aut(G)$ such that $(\pi(u),\pi(v)) = (w,x)$ and $(\pi(u),\pi(v)) = (x,w)$. Notice that this condition is stronger that the edge-transitive condition.

For instance, in the 3-path graph (see Example 4), edge $(1,2)$ is maped to vertices in edge $(2,3)$ through the permutation $\sigma =(1,3)$, it is $(\sigma(1),\sigma(2))=(3,2)$. However, there is not automorphism $\pi$ such that $(\sigma(1),\sigma(2))=(2,3)$. Therefore, the 3-path is edge-transitive but not arc-transitive. By the other hand, the square-graph (see Example 1 and 2) and the 3-complete graph (see Example 3) are arc-transitive.

In general, arc-transitive graphs are vertex and edge-transitive, however, there are vertex and edge-transitive graphs with odd degree that are not arc-transitive. These graps are called semi-simetric or half-transitive. The smallest known semi-symmetric graph is the Holt graph discovered by Derek Holt in the seventies.

t-arc-transitive graphs

A graph is t-arc-transitive, also called t-transitive, if there is an automorphism between any t-arcs but not (t+1)-arcs, i.e. for all two t-arcs $v_1,v_2,..., v_t$ and $u_1,u_2,...,u_t$, there exists $\pi \in Aut(G)$ such that $\pi(v_i)= u_i$ for $1\leq i\leq t$.

Example 6. The Möbius–Kantor graph is 2-arc-transitive.

Distance-transitive graphs

A graph is distance transitive, if there is an automorphism between any two pair of vertice that are at the same distance, i.e. for all $v_1,v_2,u_1,u_2\in V$, such that $d(v_1,v_2)=d(u_1,u_2)$, there exists $\pi \in Aut(G)$ such that $\pi(v_1)= u_1$ and $\pi(v_2)= u_2$.

Example 6. The Petersen graph is distance transitive.